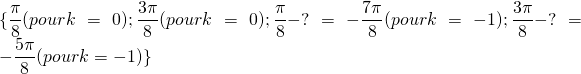Pour résoudre dans ![]() les équations de la forme
les équations de la forme ![]() où
où ![]() est donné :
est donné :
Etape 1 : vérifier que ![]() . Si c’est le cas, passer à l’étape 2, Sinon, l’équation n’admet pas de solution.
. Si c’est le cas, passer à l’étape 2, Sinon, l’équation n’admet pas de solution.
Etape 2 : Chercher un nombre ![]() tel que
tel que ![]()
Etape3 : on résout alors ![]() qui a pour solution dans
qui a pour solution dans ![]() tous les nombres de la forme
tous les nombres de la forme ![]() et
et ![]() ,
, ![]() étant un nombre entier relatif.
étant un nombre entier relatif.
Exemple :
Résoudre dans ![]() les équations suivantes :
les équations suivantes :
![]() ;
; ![]() et
et ![]() .
.
Solution :
![]() n’a pas de solution cas
n’a pas de solution cas ![]() .
.
![]() , et
, et ![]() .
.
![]() donc
donc ![]() .
.
On a alors : ![]() ou
ou ![]() ,
, ![]() , c’est-à-dire
, c’est-à-dire ![]() ou
ou ![]() ,
, ![]() .
.
![]()
![]() ou
ou ![]() ,
, ![]() .
.
![]()
Astuce
Pour déterminer l’ensemble solution d’une équation sur un intervalle donné, on ne retient que les valeurs de ![]() qui donne une solution dans l’intervalle voulu
qui donne une solution dans l’intervalle voulu
Exemple :
Les solutions de l’équation ![]() sur l’intervalle
sur l’intervalle ![]() sont :
sont :