Cas 1 : en utilisant les effectifs cumulés croissants
En utilisant le tableau des effectifs cumulés croissants, pour déterminer l’intervalle médian ou la classe médiane, il suffit de trouver la classe correspondant à la première fois où la valeur de l’effectif cumulé croissante est supérieure ou égale à la moitié de l’effectif total.
Exemple :
Considérons dans une classe de première S, la série statistique définie par le tableau suivant :
| Tailles | [1,50; 1,65[ | [1,65; 1,70[ | [1,70; 1,75[ | [1,75; 1,85[ | [1,85; 1,95[ |
| Nombre d’élève | 14 | 8 | 12 | 4 | 2 |
| Effectif cumulé croissant | 14 | 22 | 34 | 38 | 40 |
La première fois que l’effectif cumulé dépasse ![]() se trouve à la modalité
se trouve à la modalité ![]() .
.
Ainsi [1,65;1,70[ est la classe médiane ou l’intervalle médian.
Cas 2 : de manière graphique, ayant le polygone des effectifs cumulés croissants
En utilisant le polygone ou graphe des effectifs cumulés croissants, pour déterminer l’intervalle médian ou la classe médiane, il suffit de :
- Placer sur l’axe des ordonnées un point correspondant à la moitié de l’effectif total.
- Construire une droite passant par ce point et parallèle à l’axe des abscisses
- Cette droite coupe le polygone des effectifs cumulés croissants en un point, partant de ce point, construire une nouvelle droite passant par ce point et parallèle à l’axe des ordonnées.
- Cette dernière droite coupe l’axe des abscisses en un point Me, c’est la médiane de la série statistique. Et la classe modale à laquelle appartient cette valeur Me est la classe médiane ou l’intervalle médian.
Exemple
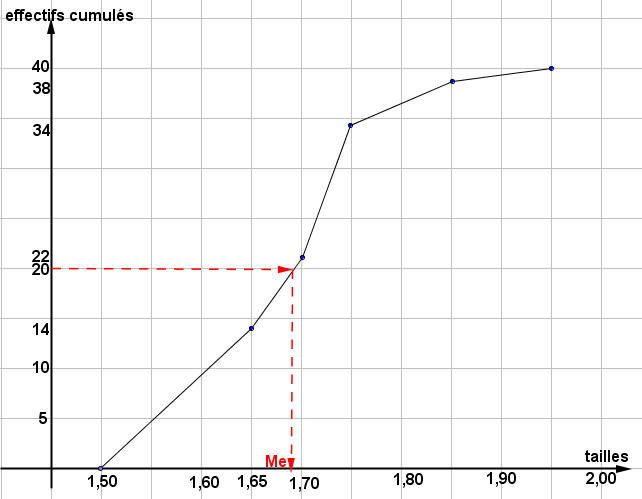
Considérons le graphe représenté plus bas.
De cette représentation du polygone des effectifs cumulés croissants, on observe que Me appartient à la classe [1,65;1,70[
Donc [1,65;1,70[ est la classe médiane de la série statistique.
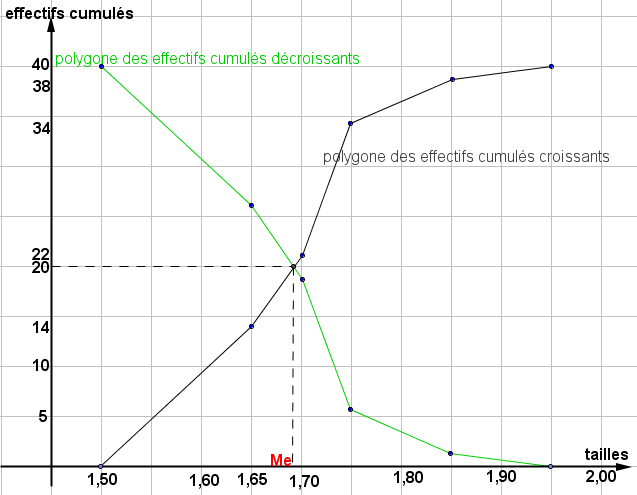
Cas 3 : de manière graphique, ayant le polygone des effectifs cumulés croissantes et décroissantes sur le même graphe
En utilisant le polygone ou graphe des effectifs cumulés croissants et décroissant, pour déterminer l’intervalle médian ou la classe médiane, il suffit de trouver l’abscisse du point d’intersection des deux polygones.
L’abscisse trouvée est Me la médiane de la série statistique. La classe modale à laquelle appartient cette valeur Me est la classe médiane ou l’intervalle médian.
Exemple :
En reprenant l’exemple de tout à l’heure on obtient le même résultat c’est-à-dire que Me appartient à la classe [1,65;1,70[
Donc [1,65;1,70[ est la classe médiane de la série statistique