Dans ce cas, soient ![]() et
et ![]() ces deux plans.
ces deux plans.
- On determine un vecteur normal de chaque plan
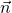 et
et 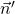 .
. - Si
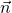 et
et 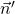 ne sont pas colinéaires alors les plans
ne sont pas colinéaires alors les plans 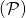 et
et 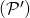 sont sécants
sont sécants - Si
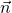 et
et 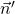 sont colinéaires alors :
sont colinéaires alors :
– Si un point quelconque de ![]() appartient à
appartient à ![]() , alors les deux plans sont confondus;
, alors les deux plans sont confondus;
– Si un point quelconque de ![]() n’appartient pas à
n’appartient pas à ![]() , alors les deux plans sont strictement parallèles.
, alors les deux plans sont strictement parallèles.
Exemple :
Etudier la position relative des plans ![]() et
et ![]() .
.
Solution
![]()
![]()
![]() et
et ![]() sont colinéaires.
sont colinéaires.
De plus ![]() et
et ![]() .
.
Donc les deux plans sont strictement parallèles.
Astuce :
Soient ![]() et
et ![]() deux plans de vecteurs normaux
deux plans de vecteurs normaux ![]() et
et ![]() .
.
Si ![]() et
et ![]() sont orthogonaux
sont orthogonaux ![]() alors
alors ![]() .
.