Soit ![]() l’univers ou l’ensemble des issues possible d’une expérience. Soit
l’univers ou l’ensemble des issues possible d’une expérience. Soit ![]() un événement.
un événement.
1/ Déterminer la probabilité de réalisation de l’événement 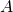 ,
,
Pour déterminer la probabilité de réalisation de l’événement ![]() , on fait la somme des probabilités de réalisation des événements élémentaires constituant l’événement
, on fait la somme des probabilités de réalisation des événements élémentaires constituant l’événement ![]() .
.
Dans le cas où les événements élémentaires ont la même « chance » d’apparaitre.
C’est-à-dire en cas d’équiprobabilité, la probabilité de ![]() ,
, ![]() c’est-à-dire, le nombre d’issues favorables à
c’est-à-dire, le nombre d’issues favorables à ![]() divisé par le nombre d’issues possibles.
divisé par le nombre d’issues possibles.
Pour déterminer la probabilité de l’événement contraire d’un événement ![]() dont on connait la probabilité d’apparition, il suffit de calculer
dont on connait la probabilité d’apparition, il suffit de calculer ![]() . Car
. Car ![]() .
.
Exemple :
1) Considérons l’expérience consistant à lancer un dé à ![]() faces numérotées de
faces numérotées de ![]() à
à ![]() (une face marquée du numéro
(une face marquée du numéro ![]() , deux faces marquées du numéro
, deux faces marquées du numéro ![]() , une face marquée du numéro
, une face marquée du numéro ![]() et les deux dernières faces marqué du numéro
et les deux dernières faces marqué du numéro ![]() ) et de noter le chiffre qui apparait.
) et de noter le chiffre qui apparait.
Déterminer la probabilité de l’événement ![]() = « obtenir un numéro pair » et celle de
= « obtenir un numéro pair » et celle de ![]() .
.
2) Considérons l’expérience consistant à lancer un dé à ![]() faces numérotées de
faces numérotées de ![]() à
à ![]() et de noter le chiffre qui apparait.
et de noter le chiffre qui apparait.
Déterminer la probabilité de l’événement ![]() = « obtenir un numéro pair » et celle de
= « obtenir un numéro pair » et celle de ![]() .
.
1) Dans ce cas les événements élémentaires n’ont pas la même probabilité d’apparition.
En effet, du fait qu’il y a deux faces marquées du chiffre ![]() augmente les chances d’apparition du chiffre
augmente les chances d’apparition du chiffre ![]() au bout d’un lancé.
au bout d’un lancé.
Comme ![]() ,
, ![]() et comme
et comme ![]()
Il suit que : ![]() .
.
On a également ![]()
2) Dans ce cas, les événements élémentaires ont la même probabilité d’apparition, c’est-à-dire qu’il y a équiprobabilité.
On a donc ![]() car
car ![]() et
et ![]() .
.
On a également ![]()
2/ Déterminer la probabilité de la réalisation de la réunion des événements A et B
Pour déterminer la probabilité de la réalisation de la réunion des événements ![]() et
et ![]() connaissant la probabilité des événements
connaissant la probabilité des événements ![]() ,
, ![]() et
et ![]() , on utilise la formule suivante :
, on utilise la formule suivante : ![]()
Exemple :
Considérons l’expérience consistant à tirer et noter le numéro de la boule tirée dans l’urne, sachant que l’urne contenant dix boules identiques au touché et numéroté de ![]() à
à ![]() . Considérons les événements
. Considérons les événements ![]() = « tirer une boule de numéro strictement inférieur à
= « tirer une boule de numéro strictement inférieur à ![]() » et
» et ![]() = « on tire une boule de numéro pair ».
= « on tire une boule de numéro pair ».
Déterminer la probabilité de ![]() .
.
Solution :
Comme les boules sont identiques, toutes les boules ont la même chance d’être tiré. Il y a donc équiprobabilité.
Il suit que :
![]() ;
;
![]()
Et ![]() car
car ![]() ;
; ![]() et
et ![]() .
.
Il en résulte que ![]() .
.
Astuces :
On peut également utiliser la formule ![]() pour calculer soit
pour calculer soit ![]() , soit
, soit ![]() soit
soit ![]() .
.
En effet, de la formule ![]() , on a :
, on a :
![]()
![]()
![]()
Exemple :
Une urne contient ![]() boules identiques au touchée numérotés de
boules identiques au touchée numérotés de ![]() à
à ![]() . Parmi lesquelles les
. Parmi lesquelles les ![]() premières sont de couleurs noires, les trois suivantes de couleur rouges et le reste de couleurs blanches.
premières sont de couleurs noires, les trois suivantes de couleur rouges et le reste de couleurs blanches.
Considérons les événements :
![]() = « la boule tirée porte un numéro pair »
= « la boule tirée porte un numéro pair »
![]() = « la boule tirée est noire »
= « la boule tirée est noire »
a) Déterminer les probabilités des événements ![]() ,
, ![]() et
et ![]()
b) Déduire la probabilité l’événement ![]() (tirer une boule ayant un numéro pair et de couleur noire)
(tirer une boule ayant un numéro pair et de couleur noire)
Solution :
a) Comme toutes les boules sont identiques au touché, il y équiprobabilité.
Il suit alors que :
![]() car
car ![]() et
et ![]() l’ensemble des boules de l’urne.
l’ensemble des boules de l’urne.
![]() car
car ![]() .
.
![]() car
car ![]()
b) Déduisons la probabilité de réalisation de l’événement ![]() :
:
![]() .
.
Ainsi, la probabilité de tirer une boule de l’urne portant un numéro pair et de couleur noire est : ![]() .
.