477319415906_1088″>Pour déduire d’un échantillon de taille 
la proportion d’un caractère étudiée au sein d’une population, on applique les étapes suivantes :
Etape 1 :
Emettre une hypothèse : « Le caractère étudié est en proportion 
au sein de la population ».
Etape 2 :
Observer la fréquence 
du caractère dans un échantillon de taille , prélevé dans la population.
Etape 3 :
Calculer l’intervalle de fluctuation 
à l’aide de , et hypothétique.
Etape 4 :
Si 
alors l’hypothèse est validée au seuil de risque 
et la proportion du caractère étudié au sein de la population est bien de .
Etape 5 :
Si 
alors l’hypothèse est rejetée et n’est pas une proportion représentative de la population.
Application de la méthode :
On considère une population de truite au sein d’une rivière. On estime que la répartition des sexes au sein de la population en conditions normales est de 
de femelles et de mâles. Cependant la pollution conduirait à un déséquilibre des sexes et favoriserait la survie des truites femelles.
On prélève 100 truites dont on détermine le sexe. on trouve 63 femelles.
On souhaite savoir si la rivière est polluée ou pas.
- L’hypothèse si l’on suppose que la rivière n’est pas polluée est que « 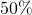de la population de truite sont des femelles », soit
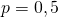. - Soit un échantillon prélevé de taille
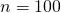truites. On observe 
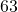femelles dans l’échantillon soit une fréquence observée de 
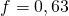. - On calcule l’intervalle de fluctuation :
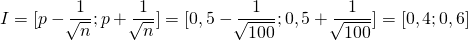. - Ainsi on observe que 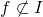, l’hypothèse est rejetée.
- Conclusion : Les proportions de truites dans les deux sexes ne sont pas les mêmes, la rivière doit donc être polluée.
id= »yui_3_17_2_1_1
