Methode 1 : Etudier les positions relatives de deux droites données par leur équations.

Pour rechercher les positions relatives de deux droites données par leur équations, on résoud le système forme par ses équations:

• si le système admet une unique solution 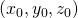alors les deux droites sont sécantes en .
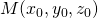• si le système admet plus d’un triplet solution alors les deux droites sont confondues.
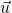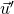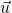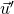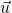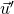• si le système n’admet pas de solution alors on considère les vecteurs et directeurs des deux droites:si et sont colinéaires alors les deux droites sont strictements parallèles;si et ne sont pas colinéaires alors les deux droites ne sont pas coplanaires.

Exemple :

Etudier les positions relatives des droites et dans chacun des cas suivants:

1)

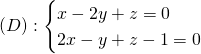
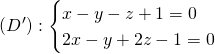
2)

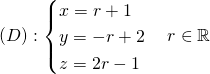
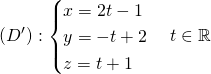
Solution

1) On résoud le système

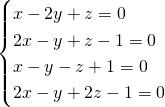
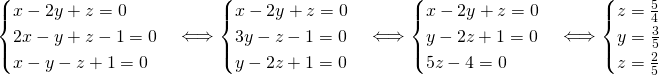
On a . Donc le système n’admet pas de solution

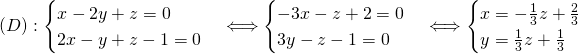
Donc un vecteur directeur de est .

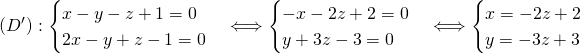
Un vecteur directeur de est . et ne sont pas colinéaires donc les droites et ne sont pas coplanaires.

2- On résoud le système

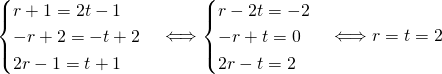
On a

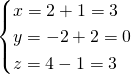
Donc et sont sécantes en .

 
 
 ses}