A. Définition
L’arbre des possibles d’une expérience aléatoire est une représentation graphique des différentes issues de l’expérience.
Le nombre de branches de l’arbre est égal au nombre d’issues.
Exemple :
Roue de la loterie
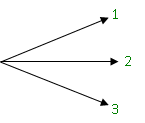
Puis pondérer l’arbre, c’est faire figurer sur chaque branche la probabilité associée :
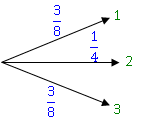
Exemple :
Une urne contient 15 boules : 2 vertes – 3 bleues – 1 rouge – 5 jaunes – 4 noires
On définit les événements élementaires suivantes :
V : « Tirer une boule verte »
B : « Tirer une boule bleue »
R : « Tirer une boule rouge »
J : « Tirer une boule jaune »
N : « Tirer une boule noire »
a) Dessiner l’arbre des possibles, le pondérer.
b) Calculer la somme des probabilités sur chaque branche.
a) arbre des possibles
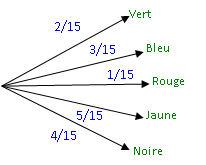
b) Somme des probabilités sur chaque branche
![]()
![]()
![]()
B. Propriété :
La somme des probabilités sur chaque branche d’un arbre est toujours égale à 1.