- On dit que
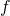admet un point d’inflexion en 
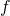si change de concavité en . C’est-à-dire que 
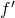change de sens de variation en - En un point d’inflexion, la courbe traverse sa tangente
Dire que 
change de sens de variation revient à dire que 
change de signe. Ainsi, en un point d’inflexion, s’annule en changeant de signe.
Comme on l’a vu plus haut, la fonction 
est concave sur 
et convexe sur 
. admet alors un point d’inflexion en 
.
