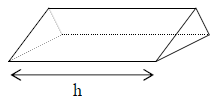
A. Prisme droit
| Définition |
Un prisme droit est un solide composé :
|
| Représentation
perspective cavalière |
|
| La hauteur d’une pyramide est la droite passant par le sommet et perpendiculaire à la base | |
| Volume |
avec |
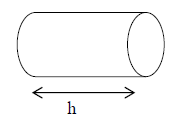
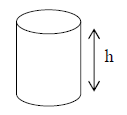
B. Cylindre de révolution
| Définition |
Une cylindre est un solide composé :
|
| Représentation
perspective cavalière |
|
| La hauteur d’un cylindre est une droite perpendiculaire aux bases | |
| Volume |
Volume = Aire de la base
|
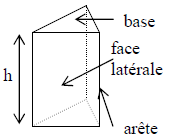
C. Pyramide
| Définition |
Une pyramide est un solide composé :
|
| Représentation
perspective cavalière |
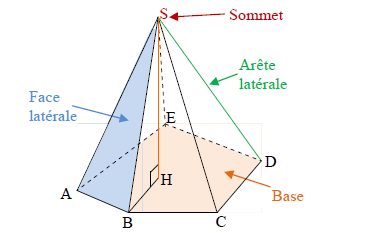 |
| La hauteur d’une pyramide est la droite passant par le sommet et perpendiculaire à la base | |
| Volume |
avec |
D. Cône de révolution
| Définition |
Un cône de révolution est un solide composé :
|
| Représentation
perspective cavalière |
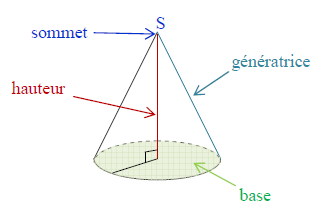 |
| La hauteur d’un cône de révolution est la droite passant par le sommet et perpendiculaire à la base | |
| Volume |
avec |