2.1 Coordonnées d’un vecteur de l’espace
Si (
, 
, 
) est une base de l’espace, alors tout vecteur 
de l’espace peut s’écrire comme combinaison linéaire des vecteurs 
et ;
c’est-à-dire qu’il existe trois nombres réels 
et 
tels que 
. 
est unique.
Le triplet est appele coordonnées du vecteur dans la base (, , ), on note 
ou 
.
Exemple :
Si 
est une base de 
et 
alors 
dans la base .
2.2 Repère de l’espace – coordonnées d’un point
, , 
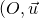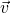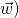est un repère de l’espace si 
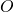est un point de l’espace appelé origine et 
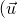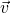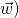, , une base.- Pour tout point
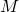de l’espace les coordonnées du vecteur 
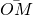dans la base 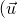, , 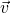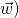sont les coordonnées du point 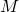dans le repère 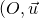, , 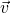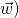. Ainsi 
, 
, 
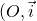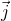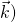est un repère de l’espace et 
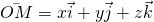alors 
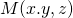dans le repère , , .
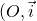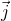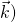Astuce :
Pour determiner les coordonnées d’un vecteur ou d’un point de l’espace, on peut utiliser la relation de Chasles et l’egalité des vecteurs.
Exemple :
Soit 
un cube, 
le milieu du segment 
.
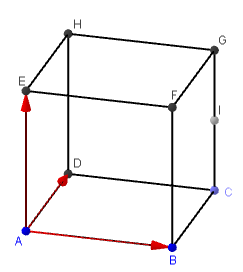
1- Determiner les coordonnées des vecteurs 
et 
dans la base 
.
2- Determiner les coordonnées de
