I. Introduction

Sujet Progress:

A. Définitions

On appelle :

Fonction affine : toute fonction qui, à tout nombre Mathplace quicklatex.com-3b8affa7af0b01fd56bf3b3eed5f262f_l3 I. Introduction , associe le nombre Mathplace quicklatex.com-49cf733129a9989dada786f7f6f6a925_l3 I. Introduction (c’est-à-dire : Mathplace quicklatex.com-452f807c98b5b518d71ef1deb429fa09_l3 I. Introduction ) où Mathplace quicklatex.com-139813192e94b132893033c54bbdb71c_l3 I. Introduction et Mathplace quicklatex.com-c7328f846d793fdd97d12ad66a3ebf64_l3 I. Introduction sont deux nombres donnés.

Fonction linéaire de coefficient Mathplace quicklatex.com-139813192e94b132893033c54bbdb71c_l3 I. Introduction : toute fonction qui, à tout nombre Mathplace quicklatex.com-3b8affa7af0b01fd56bf3b3eed5f262f_l3 I. Introduction , associe le nombre Mathplace quicklatex.com-5a1faed6164d1f29d5ae45c9225c135c_l3 I. Introduction (c’est-à-dire : Mathplace quicklatex.com-2fabaa99c94309b44a1ae19b558ec653_l3 I. Introduction ) où Mathplace quicklatex.com-139813192e94b132893033c54bbdb71c_l3 I. Introduction est un nombre donné.

Remarque :

Une fonction linéaire est un cas particulier de fonction affine. Dans ce cas, Mathplace quicklatex.com-555ac74a699db9e44fb9954e08bd2442_l3 I. Introduction

 

Exemples :

Mathplace quicklatex.com-f1528f57b43ce86c162975261f3a827f_l3 I. Introduction

La fonction f est de la forme Mathplace quicklatex.com-f4608937e0db613624862f89034ed006_l3 I. Introduction avec Mathplace quicklatex.com-b548292d86ab9fb2c396f88f16b8c998_l3 I. Introduction

Donc Mathplace quicklatex.com-01c9bfbd63c15e710ed9bdd3694581cd_l3 I. Introduction est une fonction linéaire.

Mathplace quicklatex.com-5fda046faa13a990ef47de3562fd78e7_l3 I. Introduction

La fonction g est de la forme Mathplace quicklatex.com-cdec0f5c425bcb9d6ddfdf601970dc31_l3 I. Introduction avec Mathplace quicklatex.com-86fa19cd65ef37fc9b944f4739ff1e7c_l3 I. Introduction et Mathplace quicklatex.com-45a8656ff7a739d4fcf15e3074dbe819_l3 I. Introduction

Donc Mathplace quicklatex.com-f87fdaff71b8bc3913ae3f27c24b34c5_l3 I. Introduction est une fonction affine.

 

B. Reconnaître une fonction linéaire ou affine à partir de la définition

Les fonctions suivantes représentent-elles des fonctions linéaires ou affines ?

Mathplace quicklatex.com-01d2c8974045a6fc72364b83cbb581c5_l3 I. Introduction
La fonction h n’est :

ni du type Mathplace quicklatex.com-452f807c98b5b518d71ef1deb429fa09_l3 I. Introduction

ni du type Mathplace quicklatex.com-2fabaa99c94309b44a1ae19b558ec653_l3 I. Introduction

La fonction Mathplace quicklatex.com-6f2041efb4958dcd2219e39b02d28aab_l3 I. Introduction n’est ni une fonction linéaire, ni une fonction affine.

 

Mathplace quicklatex.com-03d69261163f7be3f8ad0a63fe581621_l3 I. Introduction
La fonction k définie par Mathplace quicklatex.com-63339ad71b2db87b52b6609ab6fba12b_l3 I. Introduction peut aussi s’écrire Mathplace quicklatex.com-c73fe2a2e0d20c453128424bf083620e_l3 I. Introduction ou encore Mathplace quicklatex.com-931826644c3680d966ac42d9e1dbe614_l3 I. Introduction

On reconnait une fonction de la forme Mathplace quicklatex.com-74bfc6002a837356281b9db03013301b_l3 I. Introduction avec Mathplace quicklatex.com-e6334643c20b9dc716e0a4805f3cdb50_l3 I. Introduction et Mathplace quicklatex.com-178bd78bb40161a8705263f39434b5ef_l3 I. Introduction

Donc, Mathplace quicklatex.com-5e2d10ed2cfea6b7ca90cc035d64360c_l3 I. Introduction est une fonction affine.

 

C. Image et antécédent

Par une fonction :

  • linéaire, l’image de 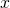Mathplace quicklatex.com-3b8affa7af0b01fd56bf3b3eed5f262f_l3 I. Introduction est Mathplace quicklatex.com-5a1faed6164d1f29d5ae45c9225c135c_l3 I. Introduction
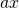
  • affine, l’image de 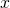Mathplace quicklatex.com-3b8affa7af0b01fd56bf3b3eed5f262f_l3 I. Introduction est Mathplace quicklatex.com-49cf733129a9989dada786f7f6f6a925_l3 I. Introduction
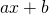
A noter :

Toutes ces phrases suivantes sont équivalentes.

Quand on écrit Mathplace quicklatex.com-7182d1edd4519388ac53d40fe45d3004_l3 I. Introduction , on peut dire que :

  • l’image de 5 par la fonction 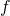Mathplace quicklatex.com-01c9bfbd63c15e710ed9bdd3694581cd_l3 I. Introduction est 10,
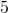  • Mathplace quicklatex.com-6e19d1fb79b0bae712c748d3614a5844_l3 I. Introduction a pour image 10 par la fonction Mathplace quicklatex.com-01c9bfbd63c15e710ed9bdd3694581cd_l3 I. Introduction ,
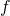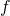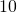  • l’antécédent de 10 est 5 par la fonction Mathplace quicklatex.com-01c9bfbd63c15e710ed9bdd3694581cd_l3 I. Introduction ,
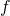  • Mathplace quicklatex.com-a740d5fb2d3c0f1c57585e81bf5c92e2_l3 I. Introduction a pour antécédent 5 par la fonction Mathplace quicklatex.com-01c9bfbd63c15e710ed9bdd3694581cd_l3 I. Introduction .