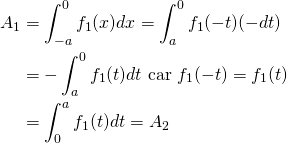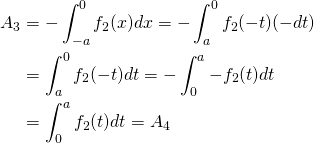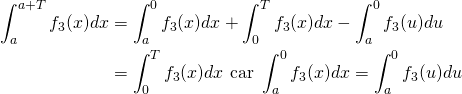Exercice 6 : Propriétés des intégrales
Figure 
Figure 
Figure 
On considère les courbes 
et 
des fonctions 
et 
respectives.
1. On suppose que 
est paire.
a) Justifier que 
.
b) En déduire que 
.
2. On suppose que 
est impaire.
a) Montrer que 
.
b) En déduire que 
.
3. On suppose que est périodique de periode 
. Montrer que 
.
et 
.
, pour 
on a 
et 
car 
et 
.
, pour 
.
et pour 
.
.