1- Soit 
la fonction définie sur 
par 
.
a) Déterminer les réels 
et 
tels que pour tout 
.
b) Trouver une primitive de sur .
2- Soit la fonction définie sur 
par 
.
a) Déterminer les réels et tels que pour tout 
.
b) Trouver alors les primitives de sur .
1- a) On a 
Ceci est égal a 
sur 
si et seulement si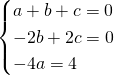 
d’ou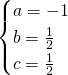 
Donc 
.
b) Une primitive 
de sur est donnée par 
.
2- a) On reduit au même denominateur et on a
Ceci est égal a sur 
si et seulement si pour tout 
de , 
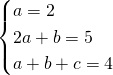
soit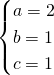 
Ainsi, sur 
.
b) D’après l’expression trouvée précédente, les primitives de sont données par $F(x) = 2x+\ln (x+1)-\frac{1}{x+1}+k, k\
