On considère les points 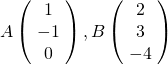 et
et 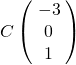 , le vecteur
, le vecteur 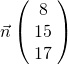 .
.
1- Vérifier que les points ![]() et
et ![]() ne sont pas alignés.
ne sont pas alignés.
2- Montrer que le vecteur ![]() est un vecteur normal du plan
est un vecteur normal du plan ![]() .
.
3- En déduire une équation cartésienne du plan ![]() .
.
On considère les points 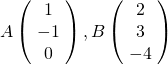 et
et 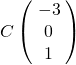 , le vecteur
, le vecteur 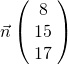 .
.
1- Vérifier que les points ![]() et
et ![]() ne sont pas alignés.
ne sont pas alignés.
2- Montrer que le vecteur ![]() est un vecteur normal du plan
est un vecteur normal du plan ![]() .
.
3- En déduire une équation cartésienne du plan ![]() .
.