On considère l’équation 
: 
1. Le réel 
est-il solution de ? Justifier la réponse.
2. Donner deux contraintes à la résolution de .
En déduire que toute solution de si elle existe, appartient à l’intervalle 
3. Justifier que résoudre revient à résoudre le système
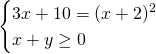
4. Résoudre l’équation .
1. n’est pas solution de car pour 
, on a : 
, impossible parce que la racine carrée d’un nombre positif est toujours positive.
2. Contraintes à la résolution de :
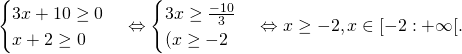
Donc toute solution de si elle existe appartient à l’intervalle 
3. 
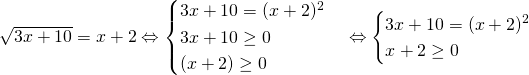
4. 
