Exercice :
Un fabricant d’un test spécifique d’une maladie fournit les caractéristiques suivantes :
- Quand la personne est malade, la probabilité pour que le test soit positif est
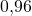. - Quand la personne n’est pas malade, la probabilité pour que le test soit négatif est de
.
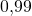Soit 
la proportion de personnes malades dans la population ciblée par le test.
On considère les événements :
M : « La personne est malade »
T : « Le test est positif »
1/ Faire un arbre pondéré de la situation
2/
a) Montrer que : 
On pose 
, 
.
b) Etudier les variations de 
sur 
c) Calculer 
; 
; 
; 
; 
; 
; 
3/
a) Montrer que 
On pose 
, .
b) Etudier les variations de 
sur
c) Calculer 
; 
; 
; 
; 
; 
; 
4/ On pose 
, .
a) Vérifier que 
et trouver les variations de 
sur .
b) Calculer 
; 
; 
; 
; 
; 
; 
5/ On pose 
, .
a) Vérifier que 
et trouver les variations de 
sur .
b) Calculer 
; 
; 
; 
; 
; 
; 
6/ Commenter les résultats obtenus.
et
.
. Donc 
.
.
.
est décroissante sur 
.
.
est croissante sur 
.
.
