On dispose d’une baguette de bois de 10 cm de long. On brise la baguette deux morceaux.
Les morceaux obtenus sont les côtés consécutifs d’un rectangle.
1. Déterminer la longueur de chaque morceau dans chacun des cas suivants :
a) L’aire du rectangle est 
b) L’aire du rectangle es 
2. Déterminer l’aire maximale d’un tel rectangle.
Soit 
la longueur et 
la largeur 
L’aire du rectangle est 
et la longueur de la baguette est 
1. On a le système :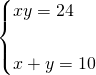 
et sont les solutions de l’équation : 
;
;
, 
Le morceau longueur mesure 
cm et le morceau largeur mesure 
cm.
2. On a le système :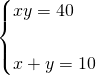 
et sont les solutions de l’équation 
Donc il est impossible de briser la baguette de telle sorte que l’aire soit 
cm
3. Soit 
l’aire de ce rectangle.
On a le système : $ \begin{cases} xy=
