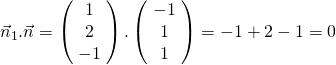On considère le plan 
d’équation 
et 
un point de l’espace.
1- Déterminer une équation cartésienne du plan 
passant 
et de vecteur normal 
.
2- Montrer que les plans et sont pérpendiculaires.
3- Calculer la distance de 
a puis a .
4- En déduire la distance de a la droite 
intersection de plans et .
car 
, donc 
.
.
.