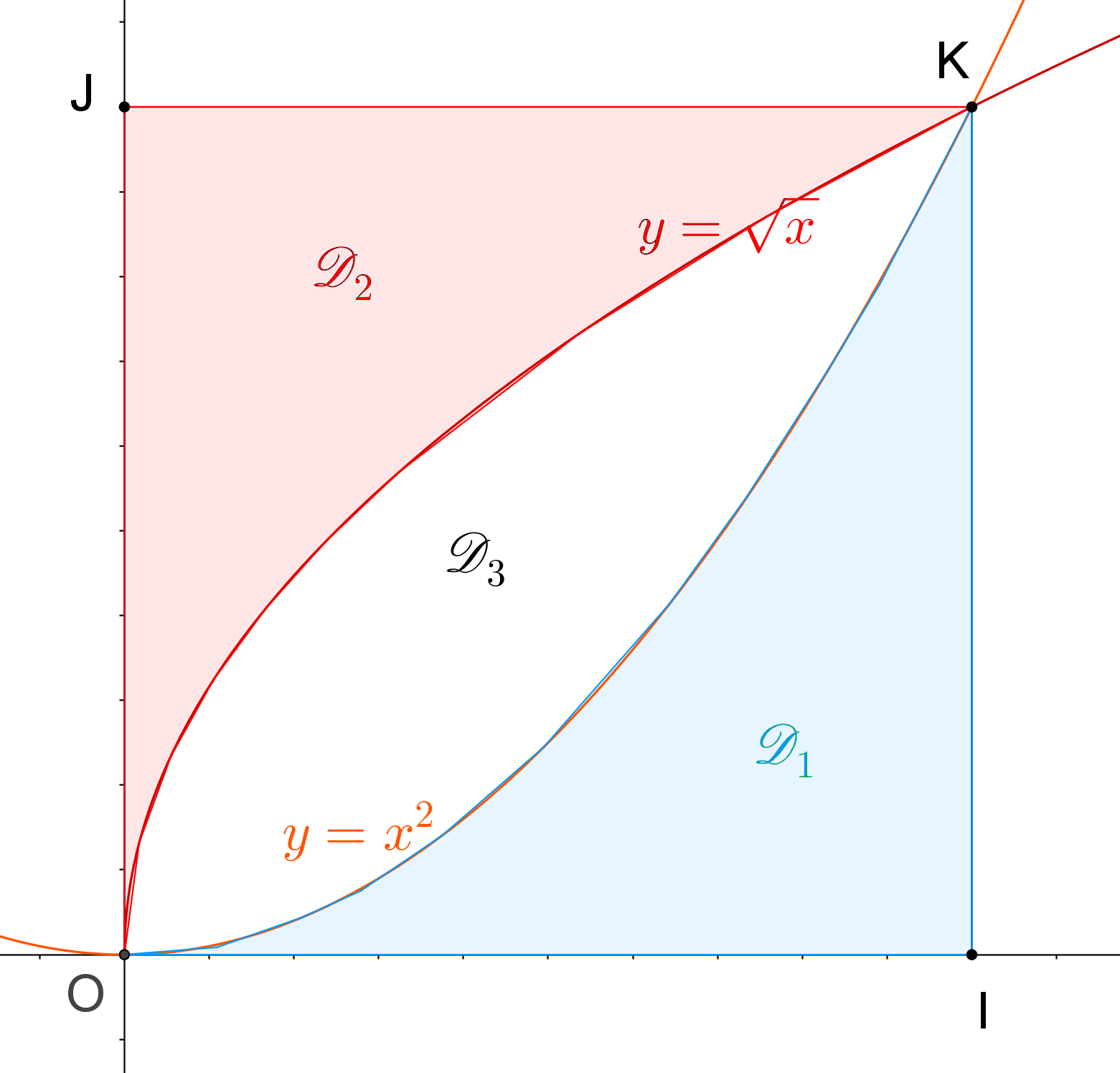
Sur la figure ci-dessus sont representées les courbes de fonctions 
et 
(
et 
respectivement). Ces courbes partagent le carré 
en trois domaines 
et 
.
1- Calculer l’aire de 
. En déduire celle de 
et celle de .
2- Ecrire l’aire de et en termes d’intégrales.
3- Quelle est la valeur de 
1- Comme sur 
, l’aire de 
en unité d’aire vaut 
La courbe représentative de vaut est l’image de celle de dans la symetrie axiale d’axe la première bissectrice des axes, c’est-a-dire la droite d’équation 
. L’aire de en unité d’aire est donc la même que celle de .
L’aire de est égale a l’aire du carré 
a laquelle on eleve les aires des domaines et . Soit une aire pour et 
d’unités d’aire.
2- a) L’aire de est l’aire de la region du plan contenant les points 
verifiant 
et 
Ceci en unité d’aire vaut 
.
L’aire de est l’aire de la region du plan délimitée par la droite d’équation 
, la courbe d’équation 
et les droites d’équations 
et 
. Elle est eqale, en unités d’aire à
par Linéarité.
b) On a donc l’égalite 
Comme 
, on obtient que $\int_0^1 \sqrt{x}dx = 1-\frac{1}{3} = \frac
