Dans un repère 
du plan, on considère les points 
, 
et 
dont les coordonnées sont : 
, 
et 
.
On pourra faire une figure.
On appelle 
et 
les points définis respectivement par : 
et 
; 
étant un réel différent de 
.
1. Déterminer les coordonnées des points et .
2.
a) Déterminer a pour que la droite 
soit parallèle a l’axe des ordonnées.
b) Déterminer une équation réduite de la droite dans le cas ou 
.
3. En déduire que le point 
, point d’intersection des droites 
et , a pour coordonnées : 
.
4. Que se passe-t-il si 
?
1/ 
.
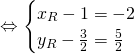
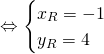Donc 
