La figure suivante est la courbe d’une fonction 
dans un repère orthonormée. La fonction est dérivable sur 
.
est son asymptote et 
sa tangente au point d’abscisse 
.
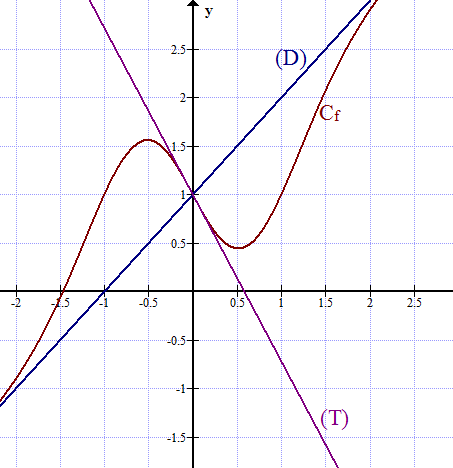
On suppose que 
1/ Déterminer une équation cartésienne de
2/ On suppose qu’il existe 
et une fonction 
définie sur telle que : 
, 
, avec 
et que 
est le centre de symétrie de 
.
a) Démontrer que 
b) En utilisant 
, montrer que : 
,
c) En déduire, après avoir exprimée 
et 
que la fonction 
est impaire
d) En déduire de la question b) que 
dérivée de est impaire.
3/ On suppose que , 
, où 
et 
sont des réels.
a) En utilisant la parité de , montrer que 
b) Calculer 
et montrer que 
en utilisant le coefficient directeur de
c) Démontrer que 
et 
.
,
donc 
.
par consequent la droite d’équation 
est asymptote à 
en 
, c’est-a-dire 
, d’ou 
est une fonction impaire.
est une fonction paire.
= 
