Equation réduite d’une droite
Théorème :
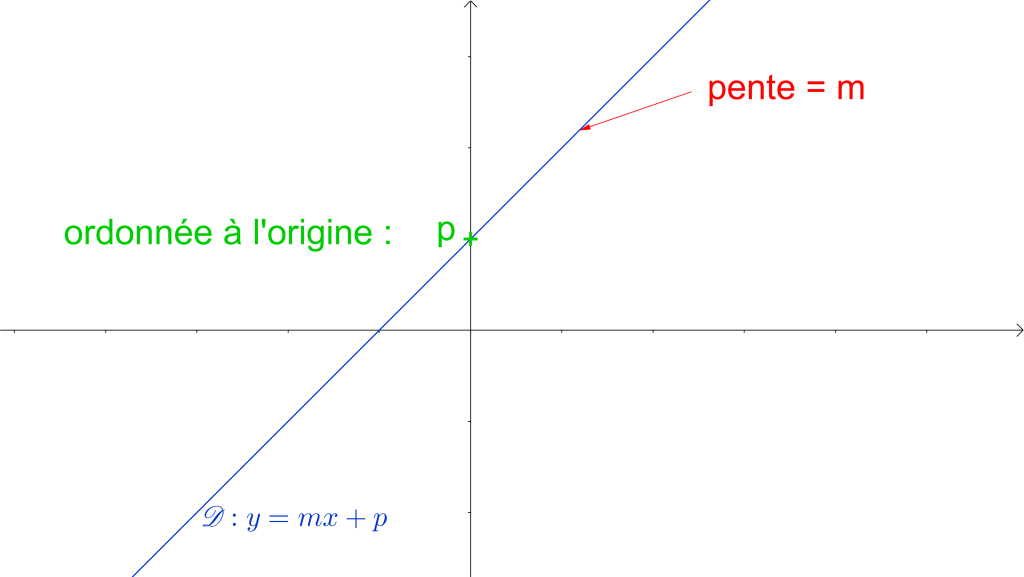
Toute droite dans un repère peut s’exprimer sous forme d’une équation appelée « équation réduite » de la forme 
.
est appelé coefficient directeur et caractérise la pente de la droite.
est l’ordonnée à l’origine.
Remarques :
- Toute droite horizontale, soit parallèle à l’axe des abscisses a une pente nulle et une équation de la forme
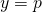avec 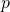constant.
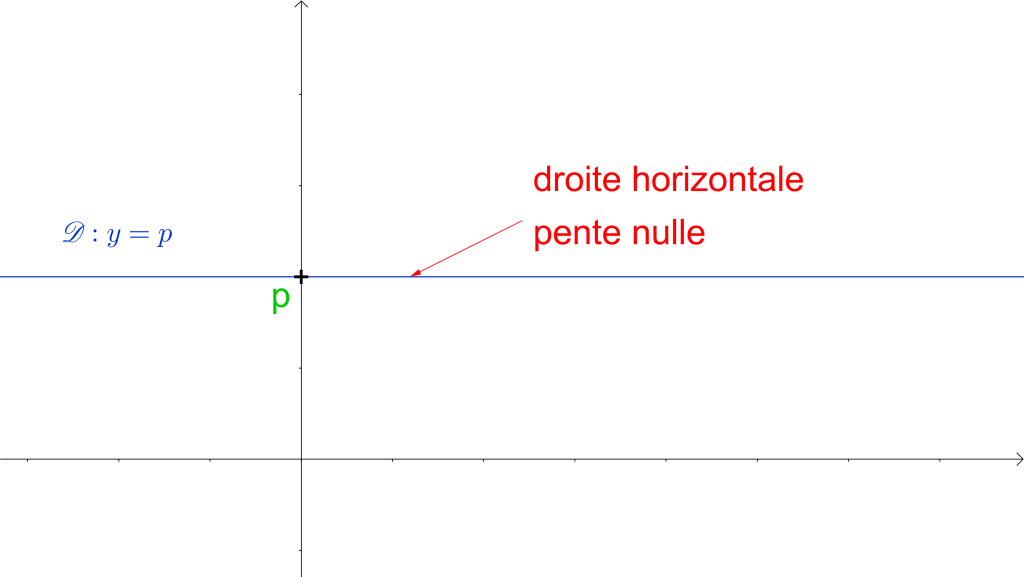
- Toute droite verticale et donc parallèle à l’axe des ordonnées a une équation de la forme
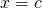avec 
une constante.
Propriété :
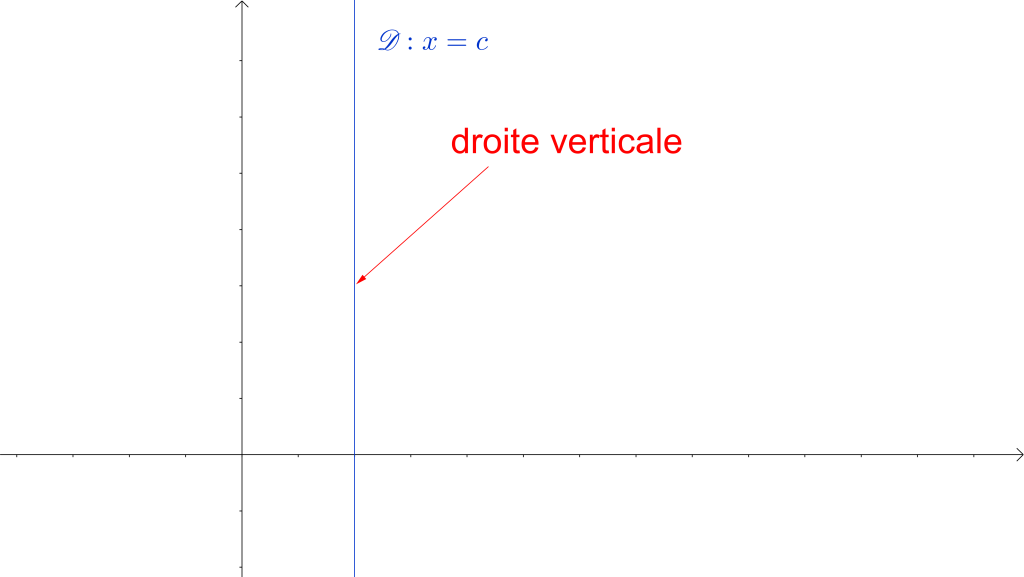
Soient deux points de coordonnées 
et 
. La droite 
a pour coefficient directeur :
