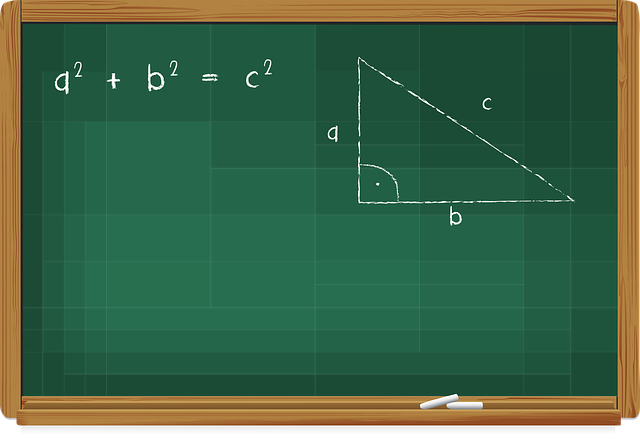
Le théorème de Pythagore est le célèbre théorème de géométrie euclidienne qui permet de mettre en relation les longueurs des côtés dans un triangle rectangle . Que dit le théorème de Pythagore :
Le carré de la longueur de l’hypoténuse, qui est le côté opposé à l’angle droit, est égal à la somme des carrés des longueurs des deux autres côtés.
Ce théorème va permettre de calculer l’une de ces longueurs à partir des deux autres. Il doit son nom à Pythagore de Samos, philosophe de la Grèce antique du VIe siècle avant J.-C. Il faut savoir tout de même que le résultat était déjà connu plus de mille ans auparavant en Mésopotamie. Rien ne permet vraiment de l’attribuer à Pythagore, même si les savants de la Grêce antique en connaissaient probablement une démonstration avant Euclide.
Les premières démonstrations historiques du théorème de Pythagore repose en général sur des méthodes de calcul d’aire par découpage et déplacement de figures géométriques. On retrouve des variantes généralisées à des triangles quelconques, à des figures de plus grande dimension telles que les tétraèdres, ou en géométrie non euclidienne comme à la surface d’une sphère.
Théorème de Pythagore ou égalité de Pythagore
Le théorème de Pythagore, vous le connaissez certainement par cœur, comme tous les élèves en classe de quatrième (4ème) au collège.
Si un triangle est rectangle, alors le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit.
Il est essentiel de ne pas oublier que le théorème s’applique uniquement sur un triangle rectangle. C’est une erreur classique que fait la plupart des élèves. Justement, il est important d’insister sur ce point car beaucoup d’erreurs d’application du théorème de Pythagore viennent de cet petit oubli.
Retenez bien cela que vous ne pouvez appliquer le théorème de Pythagore QUE pour un triangle rectangle !
Bon à savoir sur le théorème de Pythagore :
est rectangle en 
, donc l’angle est de 90°
et 
sont les cotés adjacents à l’angle droit de 90°
est le coté opposé à l’angle droit, on l’appelle aussi l’hypoténuse.
Pour bien utiliser le théorème de Pythagore, vous devez bien comprendre ces notions. Vous devez également vous assurer que vous êtes en présence d’un triangle rectangle. Pour cela, vous devez le justifier soit par l’énoncé, soit par démonstration.
Maintenant que l’on a introduit le théorème de Pythagore, voici la question importante.
A quoi il sert le théorème de Pythagore ?
Et ainsi, comment bien l’utiliser ?
Mais avant c’est quoi un théorème ? un théorème c’est une proposition énoncée que l’on peut démontrer et qui est valable quelles que soient les valeurs utilisées
Le théorème de Pythagore :
Dans un triangle rectangle : l’hypoténuse ² est égale à la somme des deux autres cotés ²
ou le carré de l’hypoténuse est égal à la somme des carrés des deux autres cotés.
Et la réciproque c’est quoi ?
Voilà un mot que pas du tout compris, et pourtant c’est tout simple, la réciproque va nous permette de démontrer l’inverse !
Alors, apprenons donc que l’on ne parle plus de théorème, ni de réciproque mais d’égalité de Pythagore.
Réciproque du Théorème de Pythagore
Dans un triangle, si le carré du plus grand des cotés (le côté opposé de l’angle droit) est égal à la somme des carrés des deux autres côtés, alors on peut dire que le triangle est rectangle.
Imaginons que l’on dispose du théorème suivant : » Si on a « A » alors on obtient « B » «
La réciproque de ce théorème serait : Si on a « B » alors on obtient « A » «
Attention !!! On ne parle de réciproque d’un théorème que dans le cas où celle-ci est vraie, pas toujours le cas.
Qu’est-ce que la contraposée d’un théorème ?
Imaginons que l’on dispose du théorème suivant : » Si on a « A » alors on obtient « B » «
La contraposée de ce théorème est : Si on n’a pas « B » alors on n’obtient pas « A » «
Contrairement à la réciproque d’un théorème, la contraposée d’un théorème est toujours vraie.
Contraposée du théorème de Pythagore
Si dans un triangle le carré de la longueur du plus grand côté n’est pas égal à la somme des carrés des deux autres autres côtés alors le triangle n’est pas rectangle.
Utilisation du théorème de Pythagore pour prouver qu’un triangle est rectangle
Si, dans un triangle, le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, alors ce triangle est un triangle rectangle.
Si 
, alors est rectangle en .
Pour avoir la méthode complète, ainsi que des exemples, rendez-vous dans le cours ici.
Lorsque l’on connaît le théorème de Pythagore et sa réciproque, on va pouvoir :
- calculer des longueurs
- calculer des angles
- démontrer que le triangle est rectangle
Si dans un devoir la question est : « Démontrer que le triangle est rectangle. Calculer la longueur du côté opposé à l’angle droit. » , vous devez avoir le réflexe d’utiliser le théorème de Pythagore !
