Comment calculer le volume d'une pyramide ?

Bonjour à tous les amateurs de mathématiques et aux élèves en quête de clarté ! En tant que professeur de mathématiques passionné depuis plus de vingt ans, je suis ravi de partager avec vous aujourd'hui mon expertise sur le calcul du volume d'une pyramide. Cette forme géométrique fascinante, qui nous rappelle les monuments égyptiens emblématiques, cache derrière son apparente complexité des formules étonnamment élégantes.

La pyramide est une figure tridimensionnelle qui a captivé l'humanité depuis des millénaires, de l'Égypte ancienne aux gratte-ciels modernes. Savoir calculer son volume n'est pas seulement un exercice académique, mais une compétence qui trouve des applications dans l'architecture, l'ingénierie, et même dans la vie quotidienne. Que vous prépariez un examen ou que vous ayez simplement besoin de cette connaissance pour un projet, cet article vous guidera pas à pas à travers les différentes méthodes et formules.

Pour avoir un apercu rapide voici un tableau récapitulatif des formules de volume pour les pyramides :

Type de pyramide	Formule de volume	Données nécessaires	Exemple d'application
Pyramide quelconque	V = (1/3) × B × h	Aire de la base (B) et hauteur (h)	Calcul général pour toute pyramide
Pyramide à base carrée	V = (1/3) × a² × h	Côté de la base (a) et hauteur (h)	Monuments pyramidaux, toits
Pyramide à base rectangulaire	V = (1/3) × L × l × h	Longueur (L), largeur (l) et hauteur (h)	Toits de bâtiments, objets décoratifs
Pyramide triangulaire (tétraèdre)	V = (1/3) × (b×h₁)/2 × h₂	Base (b) et hauteur (h₁) du triangle de base, hauteur de la pyramide (h₂)	Structures légères, modèles moléculaires
Pyramide hexagonale	V = (1/3) × (3√3/2) × a² × h	Côté de l'hexagone (a) et hauteur (h)	Cristaux, structures en nid d'abeilles

La formule fondamentale du volume d'une pyramide

La formule de base pour calculer le volume de n'importe quelle pyramide est remarquablement simple et universelle. Cette formule s'applique à toutes les pyramides, quelle que soit la forme de leur base.

Comprendre cette formule fondamentale est essentiel avant d'explorer des cas plus spécifiques.

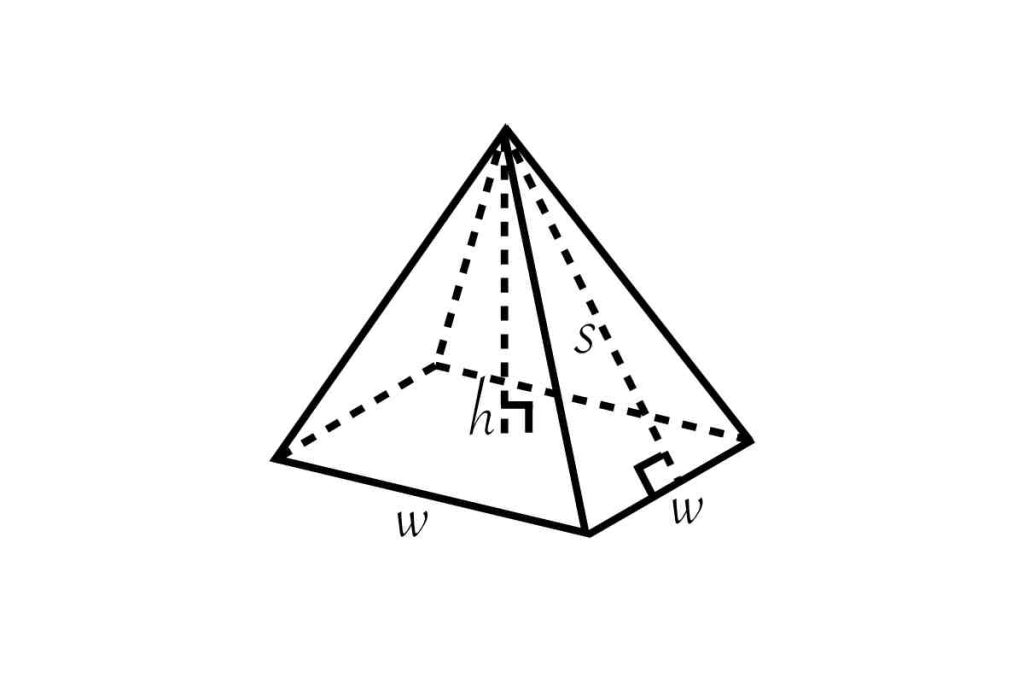
Comprendre la formule V = (1/3) × B × h

La formule du volume d'une pyramide est :

V = (1/3) × B × h

Où :

• V représente le volume de la pyramide
• B est l'aire de la base (quelle que soit sa forme)
• h est la hauteur de la pyramide (la distance perpendiculaire du sommet à la base)
• 1/3 est le facteur qui distingue le volume d'une pyramide de celui d'un prisme de même base et hauteur

Cette formule nous apprend un fait remarquable : une pyramide occupe exactement un tiers du volume d'un prisme ayant la même base et la même hauteur. Cette relation élégante a été démontrée par les mathématiciens de l'Antiquité et reste fondamentale en géométrie.

Origine et démonstration de la formule

La formule du volume de la pyramide a été établie par les mathématiciens de l'ancienne Grèce, notamment par Euclide et Archimède. La démonstration rigoureuse utilise des principes du calcul intégral, mais on peut aussi comprendre intuitivement cette relation du tiers en considérant que trois pyramides identiques peuvent être assemblées pour former un prisme.

Pour les curieux, la démonstration exacte utilise le principe de Cavalieri ou la méthode d'exhaustion, mais ce qui importe pour nos calculs est la fiabilité universelle de cette formule.

Exemple de calcul avec la formule principale

Prenons un exemple concret : calculons le volume d'une pyramide dont la base est un carré de 6 mètres de côté et la hauteur est de 8 mètres.

1. D'abord, calculons l'aire de la base carrée : B = 6² = 36 m²
2. Appliquons ensuite la formule du volume : V = (1/3) × B × h V = (1/3) × 36 × 8 V = (1/3) × 288 V = 96 m³

Le volume de cette pyramide est donc de 96 mètres cubes.

Calcul du volume selon la forme de la base

Bien que la formule fondamentale s'applique à toutes les pyramides, il peut être utile de disposer de formules spécifiques selon la forme de la base. Ces variantes facilitent les calculs directs lorsque vous connaissez les dimensions de la base plutôt que son aire.

Explorons les formules pour les types de pyramides les plus courants.

Pyramide à base carrée

Une pyramide à base carrée (comme les grandes pyramides d'Égypte) a un volume calculé par :

V = (1/3) × a² × h

Où :

• a est la longueur du côté de la base carrée
• h est la hauteur de la pyramide

Exemple de calcul pour une pyramide à base carrée

Calculons le volume d'une pyramide dont la base est un carré de 5 mètres de côté et la hauteur est de 7 mètres :

V = (1/3) × 5² × 7 V = (1/3) × 25 × 7 V = (1/3) × 175 V = 58,33 m³

Pyramide à base rectangulaire

Pour une pyramide dont la base est un rectangle, le volume se calcule par :

V = (1/3) × L × l × h

Où :

• L est la longueur de la base rectangulaire
• l est la largeur de la base
• h est la hauteur de la pyramide

Exemple de calcul pour une pyramide à base rectangulaire

Calculons le volume d'une pyramide dont la base est un rectangle de 8 mètres de longueur et 4 mètres de largeur, avec une hauteur de 6 mètres :

V = (1/3) × 8 × 4 × 6 V = (1/3) × 32 × 6 V = (1/3) × 192 V = 64 m³

Pyramide triangulaire (tétraèdre)

Une pyramide triangulaire, également appelée tétraèdre, a une base triangulaire. Son volume se calcule par :

V = (1/3) × Btriangle × h

Où :

• Btriangle est l'aire de la base triangulaire (= b×h₁/2, où b est la base du triangle et h₁ sa hauteur)
• h est la hauteur de la pyramide

Exemple de calcul pour un tétraèdre

Calculons le volume d'un tétraèdre dont la base est un triangle équilatéral de 6 cm de côté (avec une hauteur triangulaire d'environ 5,2 cm) et une hauteur de pyramide de 8 cm :

1. Calculons d'abord l'aire de la base triangulaire : Btriangle = (6 × 5,2) / 2 = 15,6 cm²
2. Appliquons la formule du volume : V = (1/3) × 15,6 × 8 V = (1/3) × 124,8 V = 41,6 cm³

Exercices pratiques sur le calcul du volume d'une pyramide

Mettons en pratique ces formules avec quelques exercices ciblés qui renforceront votre compréhension et développeront votre habileté à calculer le volume de différents types de pyramides.

Ces exercices sont conçus pour couvrir une variété de situations et niveaux de difficulté.

Exercice 1 : Pyramide de Khéops

Énoncé : La pyramide de Khéops en Égypte a une base carrée dont le côté mesure environ 230 mètres et une hauteur initiale de 146,6 mètres. Estimez son volume original.

Solution : V = (1/3) × a² × h V = (1/3) × 230² × 146,6 V = (1/3) × 52 900 × 146,6 V = (1/3) × 7 755 140 V ≈ 2 585 047 m³

Le volume original de la pyramide de Khéops était donc d'environ 2,59 millions de mètres cubes.

Exercice 2 : Pyramide à base hexagonale

Énoncé : Une pyramide a pour base un hexagone régulier de 10 cm de côté. Si sa hauteur est de 15 cm, calculez son volume.

Solution :

1. Calculons d'abord l'aire de l'hexagone régulier : B = (3√3/2) × a² = (3√3/2) × 10² ≈ 259,8 cm²
2. Appliquons la formule du volume : V = (1/3) × B × h V = (1/3) × 259,8 × 15 V = (1/3) × 3 897 V = 1 299 cm³

Le volume de cette pyramide est donc d'environ 1 299 cm³.

Exercice 3 : Pyramide tronquée

Énoncé : Une pyramide à base carrée dont le côté mesure 12 m et la hauteur 8 m est tronquée parallèlement à sa base à une hauteur de 5 m du sommet. Calculez le volume de la pyramide tronquée restante.

Solution :

1. Calculons le volume de la pyramide originale complète : V1 = (1/3) × 12² × 8 = (1/3) × 144 × 8 = 384 m³
2. Déterminons le côté de la base supérieure de la section tronquée (par similitude) : Le rapport des hauteurs est (8-5)/8 = 3/8 Donc le côté de la petite base est 12 × 3/8 = 4,5 m
3. Calculons le volume de la petite pyramide enlevée : V2 = (1/3) × 4,5² × 3 = (1/3) × 20,25 × 3 = 20,25 m³
4. Le volume de la pyramide tronquée est la différence : V = V1 - V2 = 384 - 20,25 = 363,75 m³

Le volume de la pyramide tronquée est donc de 363,75 m³.

Relations géométriques avancées des pyramides

Au-delà des formules de base, les pyramides possèdent des propriétés géométriques fascinantes qui enrichissent notre compréhension de ces solides et peuvent faciliter certains calculs dans des situations spéciales.

Ces relations avancées sont particulièrement utiles pour résoudre des problèmes complexes ou pour approfondir la compréhension théorique.

Relation entre l'arête latérale et la hauteur

Dans une pyramide régulière (dont la base est un polygone régulier), il existe une relation importante entre la hauteur (h), l'apothème de la base (a) et l'arête latérale (l) :

l² = h² + a²

Cette relation dérive du théorème de Pythagore et permet de calculer l'un de ces éléments si les deux autres sont connus.

Le théorème d'Euler pour les polyèdres

Les pyramides, comme tous les polyèdres simples, obéissent au théorème d'Euler qui établit que :

S - A + F = 2

Où :

• S est le nombre de sommets
• A est le nombre d'arêtes
• F est le nombre de faces

Pour une pyramide à base n-gonale, nous avons :

• Sommets : n + 1
• Arêtes : 2n
• Faces : n + 1

Ce qui vérifie bien la relation d'Euler : (n+1) - 2n + (n+1) = 2

Applications pratiques du calcul du volume pyramidal

Le calcul du volume d'une pyramide trouve de nombreuses applications concrètes dans divers domaines. Ces exemples montrent l'importance pratique de maîtriser cette compétence mathématique.

Ces applications concrètes donnent du sens aux formules mathématiques et montrent leur utilité dans le monde réel.

Applications en architecture et construction

Le volume pyramidal est essentiel dans plusieurs aspects de l'architecture :

• Conception de toits pyramidaux pour déterminer les matériaux nécessaires
• Construction de monuments ou structures pyramidales
• Évaluation du poids et de la stabilité des structures en forme de pyramide
• Calcul du volume de béton nécessaire pour des fondations pyramidales

Applications en emballage et design

Les formes pyramidales sont également courantes dans :

• Conception d'emballages de luxe (chocolats, parfums)
• Design de récipients pour optimiser l'utilisation de l'espace
• Fabrication de boîtes-cadeaux pyramidales
• Conception de présentoirs commerciaux à forme pyramidale

Pour explorer d'autres calculs de volumes :

• Comment calculer le volume d'un cylindre
• Comment calculer un volume

Méthode expérimentale pour vérifier le volume d'une pyramide

Une façon fascinante de confirmer la formule du volume d'une pyramide est de réaliser une expérience pratique. Cette approche est particulièrement utile pour les enseignants ou pour ceux qui aiment apprendre par l'expérimentation.

Cette méthode concrète aide à visualiser et comprendre intuitivement la relation volumique entre une pyramide et un prisme.

Expérience avec modèles physiques

Vous pouvez réaliser cette expérience simple :

1. Construisez ou procurez-vous un prisme droit et une pyramide ayant exactement la même base et la même hauteur
2. Remplissez la pyramide de sable, de riz ou d'eau
3. Versez le contenu dans le prisme
4. Répétez l'opération deux fois de plus

Vous constaterez qu'il faut exactement trois pyramides pour remplir complètement le prisme, confirmant visuellement que le volume de la pyramide est un tiers de celui du prisme correspondant.

Applications pédagogiques de cette méthode

Cette approche expérimentale présente plusieurs avantages pour l'enseignement :

• Elle rend concret un concept mathématique abstrait
• Elle permet aux apprenants de découvrir par eux-mêmes la relation du tiers
• Elle offre une vérification intuitive de la formule
• Elle stimule la curiosité scientifique et l'esprit critique

Erreurs courantes à éviter dans le calcul du volume d'une pyramide

Lors du calcul du volume d'une pyramide, certaines erreurs fréquentes peuvent survenir et conduire à des résultats incorrects. En identifiant ces pièges, vous pourrez les éviter et assurer la précision de vos calculs.

Ces conseils pratiques vous aideront à vérifier si votre calcul est cohérent et logique.

Confusions courantes à éviter

• Oublier le facteur 1/3 : l'erreur la plus commune est d'omettre ce facteur essentiel
• Confondre hauteur de la pyramide et hauteur de la base : la hauteur h de la formule est toujours la distance perpendiculaire du sommet à la base
• Utiliser la mauvaise formule pour l'aire de la base : vérifiez toujours quelle formule correspond à la forme de votre base
• Erreurs d'unités : mélanger différentes unités de mesure (par exemple, base en cm² et hauteur en m)
• Confondre pyramide et cône : bien que leurs formules de volume soient similaires, les calculs de l'aire de la base diffèrent

Astuces pour vérifier vos calculs

Pour vous assurer que votre calcul du volume d'une pyramide est correct :

1. Vérifiez les dimensions : toutes les mesures sont-elles cohérentes et dans la même unité ?
2. Contrôlez l'aire de la base : avez-vous utilisé la bonne formule pour la forme de votre base ?
3. N'oubliez pas le 1/3 : cette fraction est essentielle dans la formule
4. Estimation rapide : essayez d'estimer grossièrement le volume pour voir si votre résultat est dans un ordre de grandeur raisonnable

Conclusion : maîtrisez le calcul du volume pyramidal

Nous voilà arrivés au terme de notre exploration du calcul du volume d'une pyramide. Comme vous l'avez découvert, cette forme géométrique fascinante, qui a inspiré certaines des plus grandes réalisations architecturales de l'humanité, repose sur une formule remarquablement élégante et simple dans son principe.

La beauté de la formule V = (1/3) × B × h réside dans son universalité : elle s'applique à toute pyramide, quelle que soit la forme de sa base. Cette relation du tiers avec le prisme correspondant est l'une des harmonies mathématiques qui structurent notre compréhension de l'espace tridimensionnel.

J'espère que cet article vous a permis de comprendre en profondeur le concept du volume pyramidal et ses multiples facettes. Avez-vous une application particulière en tête où ces calculs vous seraient utiles ? Rencontrez-vous encore des difficultés avec certains aspects de ces calculs ? N'hésitez pas à partager votre expérience en commentaire, je serais ravi d'échanger avec vous et de vous aider à progresser dans votre compréhension des mathématiques !